Как недавнего выпускника буткемпа по машинному обучению от Flatiron School меня буквально затопило советами о том, как стать асом в прохождении интервью. Я заметил, что из социальных компетенций чаще всего упоминают умение объяснять принципы работы сложных алгоритмов машинного обучения человеку, который в этом совершенно не разбирается.
В этой статье я поделюсь тем, как я рассказал бы об этих алгоритмах своей бабушке. В некоторых объяснениях я зайду довольно глубоко, в некоторых лишь пройдусь поверхностно по алгоритму. Надеюсь, что всё из этого будет понятно и полезно тем, кто никогда в жизни не занимался анализом данных. Рассмотрим три темы:
- Градиентный спуск и линия наилучшего соответствия.
- Линейная регрессия (включая регуляризацию).
- Логистическая регрессия.
Прежде всего, давайте разберёмся, в чём разница между алгоритмом и моделью. Хорошее объяснение есть на Quora:
Модель — как автомат с едой, который получает что-то за вход (деньги) и выдаёт какие-то выходные значения (например, газировку)… Алгоритм — это то, как обучается модель принимать решение в зависимости от входных данных. Например, алгоритм на основе ценности денег, которыми вы расплатились в автомате, и стоимости выбранного продукта будет определять, достаточно ли денег для покупки и какую сдачу вы должны получить.
То есть алгоритм — это математическая сила, стоящая за моделью. Одна и та же модель может использовать разные алгоритмы, что и будет их отличать. Алгоритм же без модели — математические уравнения, которые практически ничего не значат.
Градиентный спуск и линия наилучшего соответствия
(Хоть первое и не считается алгоритмом машинного обучения, его понимание важно для понимания того, как происходит оптимизация алгоритмов)
И вот объяснения:
Суть градиентного спуска в том, что он позволяет нам найти самое точное предсказание на основе данных.
Скажем, у тебя есть большой список роста и веса людей, которых ты знаешь, и тебе нужно каким-то образом отобразить данные на графике. Это будет выглядеть как-то так:
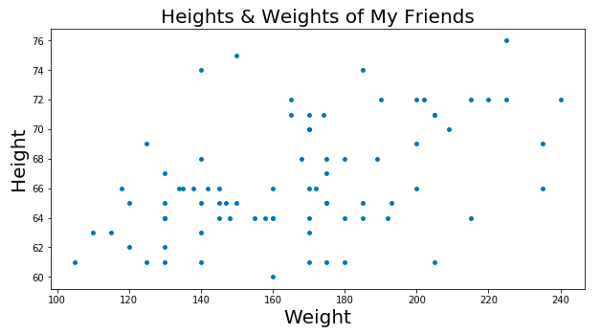 Наш выдуманный набор роста и веса (по-странному геометричный)
Наш выдуманный набор роста и веса (по-странному геометричный)Теперь допустим, что проходит соревнование. Его суть заключается в том, что участникам нужно угадать вес человека по его росту. Угадавший получает денежный приз. Кроме того, чтобы оценивать вес человека на глаз, ты бы опиралась на набор данных о твоих знакомых, да?
Так, основываясь на графике выше, скорее всего, ты бы могла дать ответ, близкий к правильному, если бы у тебя был график тренда данных. Этот график-линия показывал бы ожидаемый вес для каждого значения роста. Тогда ты бы просто нашла значение роста, двигаясь параллельно оси весов, дошла бы до линии тренда и определила бы вес, понятно?
Но как найти эту идеальную линию? Возможно, ты могла бы построить ее вручную, но это заняло бы кучу времени. Здесь и нужен градиентный спуск!
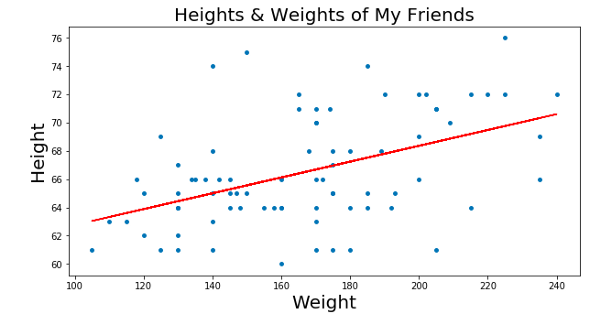 Линия наилучшего соответствия показана красным
Линия наилучшего соответствия показана краснымМы ищем эту линию при помощи минимизации так называемой “остаточной суммы квадратов”. Это просто сумма квадратов разности между значением нашей линии и точек, то есть то, насколько точки далеки от линии. Мы получаем всё меньшие значения суммы квадратов, меняя положение линии на графике: нам надо поместить нашу линию куда угодно, главное, чтобы она была как можно ближе к большинству точек.
Мы можем углубиться в это и обозначить каждый из параметров линии на кривой стоимости. При помощи градиентного спуска мы достигаем минимума кривой стоимости, где и находится минимум остаточной суммы квадратов.
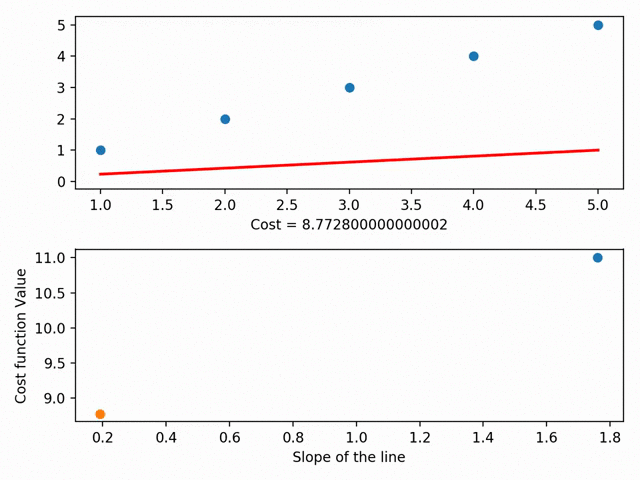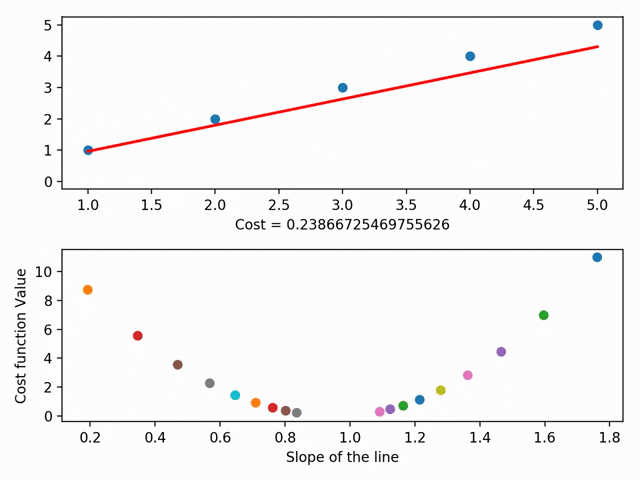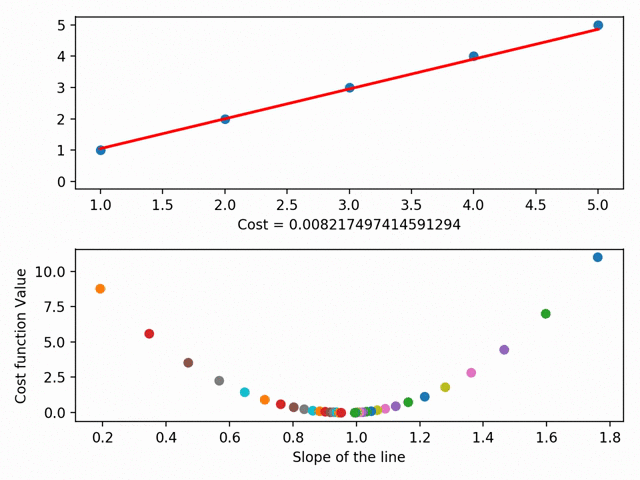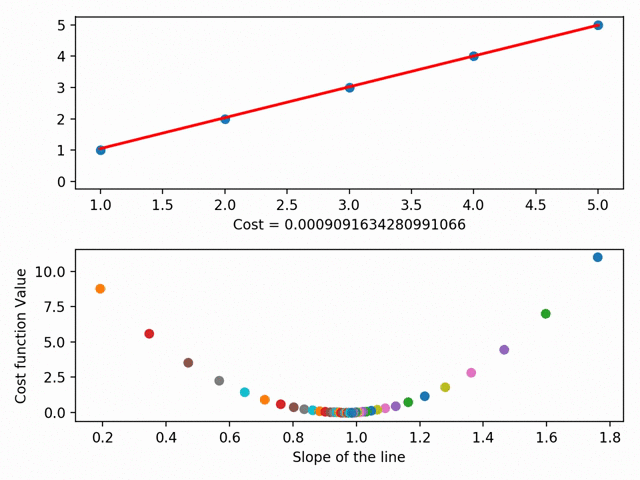 Визуализация градиентного спуска (при помощи Matplotlib)
Визуализация градиентного спуска (при помощи Matplotlib)У градиентного спуска есть ещё множество параметров, например, размер шага (то есть насколько быстро мы хотим достичь низа скейтбордной рампы) или скорость обучения (то, в каком направлении мы хотим достичь низа). В общем, суть такова: градиентный спуск позволяет найти линию наилучшего соответствия при помощи минимизации расстояния между точками графика и линией. Линия же, в свою очередь, позволяет предсказывать необходимое.
Линейная регрессия
Всё просто: линейная регрессия — это то, как мы анализируем силу зависимости между одной переменной (“результирующая переменная”) и одной или несколькими другими переменными (“независимыми переменными”).
Характерная черта линейной регрессии, как понятно из названия, заключается в том, что связь между этими переменными линейная. Что это значит в нашем случае: когда мы строим график зависимости независимых переменных от результирующей, точки будут располагаться примерно на одной линии, как показано ниже.
(Если ты не можешь построить график, то попробуй ответить на вопрос: изменение независимых переменных на определённую величину вызывает в результирующей переменной изменение на ту же величину? Если да, то данные линейно зависимы.)
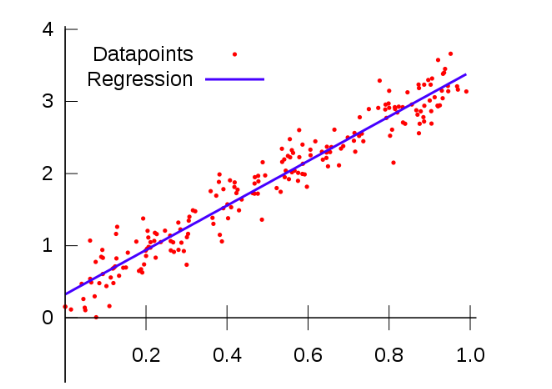 Это чем-то напоминает то, что мы делали ранее, потому что линия наилучшего соответствия и есть “линия регрессии” в линейной регрессии. Линия показывает наилучшее линейное отношение между точками, что, в свою очередь, позволяет предсказывать.
Это чем-то напоминает то, что мы делали ранее, потому что линия наилучшего соответствия и есть “линия регрессии” в линейной регрессии. Линия показывает наилучшее линейное отношение между точками, что, в свою очередь, позволяет предсказывать.Ещё одна важная деталь: результирующая переменная или то, что меняется с изменением наших других переменных, непрерывна. Что это значит?
Скажем, мы хотим измерить зависимость количества осадков от высоты над уровнем моря в штате Нью-Йорк. Тогда наша результирующая переменная — дождливость, независимая переменная — высота над уровнем моря. Если будем использовать линейную регрессию, то результирующую переменную нужно сформулировать как, например, “сколько дюймов осадков выпадает за определённое количество времени”, а не “дождливо/не дождливо”. Наша результирующая переменная должна быть непрерывной — значит она может быть любым числом (даже дробным).
Самое классное в линейной регрессии — это то, что она может предсказывать, используя линию наилучшего соответствия! Если мы запустим линейную регрессию на нашей задаче, мы можем найти эту линию, как и в градиентном спуске. Затем мы можем применять обученную модель для того, чтобы узнать количество осадков на определённой высоте.
Специально для сайта ITWORLD.UZ. Новость взята с сайта NOP::Nuances of programming
