Как реализовать древовидную сортировку в стандартной библиотеке Go

Golang

Двоичная куча

Итак, двоичная куча — это:

  • Контейнер, предоставляющий свой максимальный элемент за время O(1), добавляющий элемент за O(log n) и удаляющий максимальный элемент за O(log n).
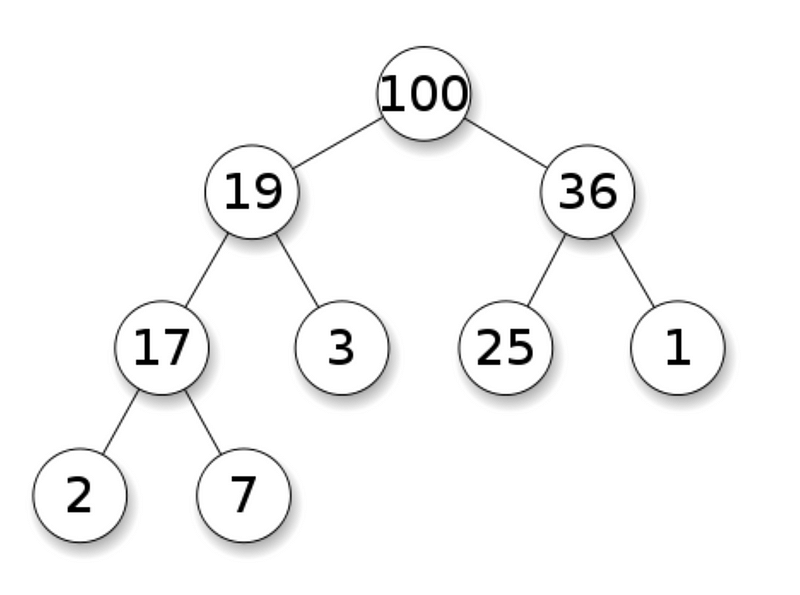
  • Неполное бинарное дерево, каждый узел которого больше или равен своим дочерним элементам. На это свойство кучи я буду ссылаться на протяжении всей статьи.

Эти свойства и определяют двоичную кучу:

Двоичная куча

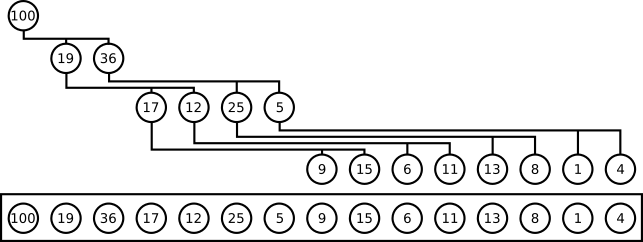
В алгоритмах кучи двоичная куча представляется как массив. В представлении массивом дочерние элементы узла с индексом i расположены в индексах 2*i+1 и 2*i+2. Вот так он выглядит:

Двоичная куча в виде массива.

Формируем кучу

Массив может быть преобразован в двоичную кучу за время O(n). Здорово, правда? Вот алгоритм:

  1. Обрабатываем входной массив как кучу. Важно: массив ещё не стал кучей.
  2. Итерируем вершины кучи, начиная с предпоследнего уровня — это на один уровень выше листа — назад к корню.
  3. Каждый обрабатываемый узел отправляйте вниз по куче, пока он не станет больше обоих дочерних элементов. Всегда меняйте его местами с наибольшим дочерним элементом. Готово!

Почему это работает?

  • Возьмите узел дерева x. Мы итерируем кучу от конца к началу. Когда мы достигнем конца, поддеревья, имеющие корни в обоих своих дочерних элементах, уже удовлетворяют свойству кучи.
  • Если x больше обоих дочерних элементов— готово.
  • Если нет, заменяем x большим дочерним элементом. Это приведет к тому, что новый корень будет больше, чем оба дочерних элемента.
  • Если x не удовлетворяет свойству кучи в новом поддереве, процесс нужно повторять до тех пор, пока результат не будет удовлетворять свойству кучи, или поддерево не станет листом, то есть у него не будет ни одного дочернего элемента.

Это верно для всех узлов в куче, включая корень.

Древовидная сортировка

Древовидная сортировка работает в 2 этапа:

  1. Формирует двоичную кучу из массива, используя вышеописанный алгоритм. Это занимает время O(n).
  2. Вставляет элементы из кучи в выходной массив, заполняя его с начала и с конца. Каждое удаление максимального элемента из кучи занимает время O(log n), что в сумме составляет O(n * log n) для всего контейнера.

Примечательное свойство реализации Go в том, что входной массив используется для хранения выходных данных, а значит, не нужно выделять память О(n) для этих данных.

Реализация

Библиотека сортировки Go поддерживает любую коллекцию, которая проиндексирована целыми числами, имеет определенный порядок элементов и поддерживает замену элементов между двумя индексами:

type Interface interface {	// Len - количество элементов в группе.	Len() int	// Less сообщает, должен ли элемент с индексом i            // быть отсортирован перед элементом с индексом j.	Less(i, j int) bool 	// Swap меняет местами элементы с индексами i и j.	Swap(i, j int)}

Ссылка на код выше.

Естественно, любой непрерывный контейнер чисел удовлетворяет этому интерфейсу.

Давайте посмотрим на тело метода heapSort():

func heapSort(data Interface, a, b int) {	first := a	lo := 0	hi := b - a	// Формирует кучу с наибольшим элементом в вершине. 	for i := (hi - 1) / 2; i >= 0; i-- {		siftDown(data, i, hi, first)	}	// Вставляет элементы, сперва наибольшие, в конец кучи. 	for i := hi - 1; i >= 0; i-- {		data.Swap(first, first+i)		siftDown(data, lo, i, first)	}}

Ссылка на код выше.

Возможно, выглядит немного загадочно, но первые 3 строки проясняют все:

  • a и b — индексы в data. heapSort(data, a, b) сортирует data в полуоткрытое множество [a, b).
  • first — это копия a.
  • lo и high — индексы, нормированные поa: lo всегда начинается с нуля. hi начинается с размера ввода.

Далее код формирует двоичную кучу:

// Формирует кучу с наибольшим элементом в вершине.for i := (hi - 1) / 2; i >= 0; i-- {  siftDown(data, i, hi, first)}

Как мы видели ранее, код проверяет кучу с уровня выше листьев и использует siftDown() для перемещения текущего элемента вниз, пока он не будет соответствовать свойству кучи. Более детально я расскажу о siftDown() ниже. На этом этапе data — это двоичная куча. Добавим все элементы, чтобы создать отсортированный массив.

// Добавляет элементы, сначала наибольшие, в конец кучи. for i := hi - 1; i >= 0; i-- {  data.Swap(first, first+i)  siftDown(data, lo, i, first)}

В этой цикле i — последний индекс кучи. В каждой итерации:

  • Максимум кучи first меняется местами с ее последним элементом.
  • Свойство кучи восстанавливается перемещением нового first вниз до тех пор, пока он не будет удовлетворять свойству кучи.
  • Размер кучи i уменьшается на один.

Другими словами, мы заполняем массив от конца к началу, двигаясь от наибольшего элемента к наименьшему, в результате получая отсортированный массив.

Восстановление свойства кучи

Для восстановления свойства кучи используетсяsiftDown(). Давайте посмотрим, как он работает.

// siftDown применяет свойство кучи к данным [lo, hi)./* first - это ответвление внутри массива, в котором лежит корень кучи. */func siftDown(data Interface, lo, hi, first int) {	root := lo	for {		child := 2*root + 1		if child >= hi {			break		}		if child+1 < hi && data.Less(first+child, first+child+1) {			child++		}		if !data.Less(first+root, first+child) {			return		}		data.Swap(first+root, first+child)		root = child	}}

Ссылка на код выше.

Этот код перемещает элемент root вниз по дереву, пока он не станет больше обоих дочерних элементов. При переходе на уровень ниже элемент заменяется наибольшим из дочерних. Убеждаемся в том, что родительский узел больше обоих дочерних элементов:

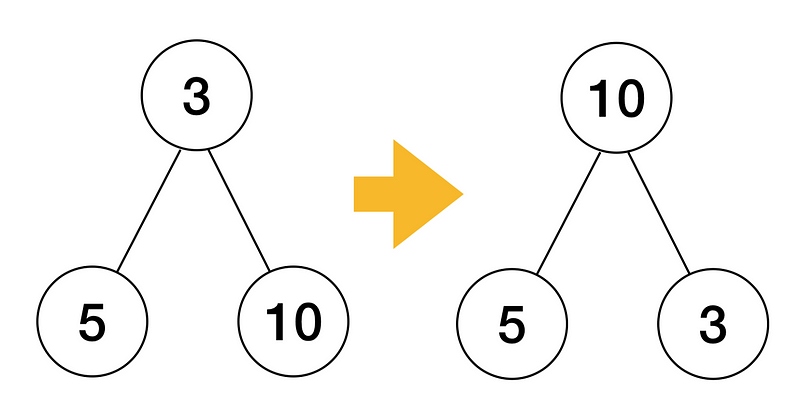Родительский элемент 3 заменяется на наибольший дочерний элемент 10

Первые несколько строк считают индекс первого дочернего элемента и проверяют его существование:

child := 2*root + 1if child >= hi {  break}

child >= hi означает, что текущий root — лист, поэтому алгоритм останавливается. Далее выбираем наибольший из двух дочерних элементов:

if child+1 < hi && data.Less(first+child, first+child+1) {  child++}

Так как любые дочерние элементы узла находятся рядом в массиве, child++ выбирает второй дочерний элемент. Далее мы проверяем, действительно ли родительский элемент меньше дочернего:

if !data.Less(first+root, first+child) {  return}

Если родительский элемент больше, чем наибольший из дочерних, мы закончили.

Наконец, если родительский элемент меньше, чем дочерний, мы меняем местами два элемента и увеличиваем root для подготовки к следующей итерации:

data.Swap(first+root, first+child)root = child

Специально для сайта ITWORLD.UZ. Новость взята с сайта NOP::Nuances of programming