Общий финансовый анализ на Python (Часть 1)

В прошлой статье рассмотрено как можно получить информацию по финансовым инструментам. Дальше будет опубликовано несколько статей о том, что первоначально можно делать с полученными данными, как проводить анализ и составлять стратегию. Материалы составлены на основании публикаций в иностранных источниках и курсах на одной из онлайн платформ.

В этой статье будет рассмотрено, как рассчитывать доходность, волатильность и построить один из основных индикаторов.

import pandas as pd
import yfinance as yf
import numpy as np
import matplotlib.pyplot as plt

sber = yf.download('SBER.ME','2016-01-01')

Доходность

Данная величина представляет собой процентное изменение стоимости акции за один торговый день. Оно не учитывает дивиденды и комиссии. Его легко рассчитать используя функцию pct_change () из пакета Pandas.

Как правило используют лог доходность, так как она позволяет лучше понять и исследовать изменения с течением времени.

# Скорректированая цена закрытия`
daily_close = sber[['Adj Close']]

# Дневная доходность
daily_pct_change = daily_close.pct_change()

# Заменить NA значения на 0
daily_pct_change.fillna(0, inplace=True)

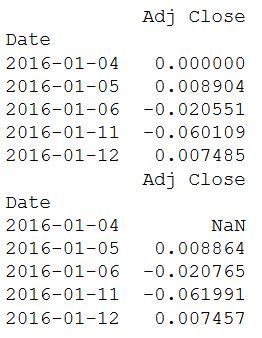
print(daily_pct_change.head())

# Дневная лог доходность
daily_log_returns = np.log(daily_close.pct_change()+1)

print(daily_log_returns.head())

Чтобы из полученных данных узнать недельную и/или месячную доходность, используют функцию resample().

# Взять у `sber` значения за последний рабочий день месяца
monthly = sber.resample('BM').apply(lambda x: x[-1])

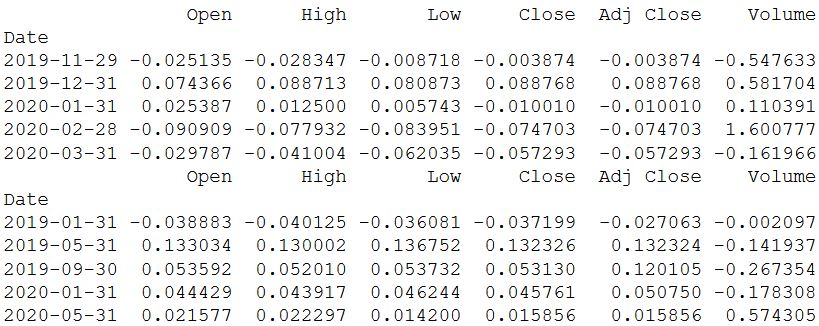
# Месячная доходность
print(monthly.pct_change().tail())

# Пересчитать `sber` по кварталам и взять среднее значение за квартал
quarter = sber.resample("4M").mean()

# Квартальную доходность
print(quarter.pct_change().tail())

Функция pct_change () удобна для использования, но в свою очередь скрывает то, как получается значение. Схожее вычисление, которое поможет понять механизм, можно выполнить при помощи shift() из пакета из пакета Pandas. Дневная цена закрытия делится на прошлую (сдвинутую на один) цену и из полученного значения вычитается единица. Но есть один незначительный минус – первое значение в результате получается NA.

Расчет доходности основан на формуле:

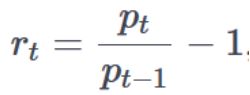
Где, p – цена, t – момент времени и r – доходность.

Дальше строится диаграмма распределения доходности и рассчитывается основная статистика:

# Дневная доходность
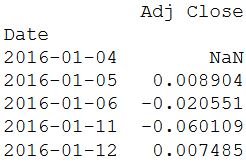
daily_pct_change = daily_close / daily_close.shift(1) - 1

print(daily_pct_change.head())

# Диаграмма `daily_pct_c`
daily_pct_change.hist(bins=50)

plt.show()

# Общая статистика
print(daily_pct_change.describe())

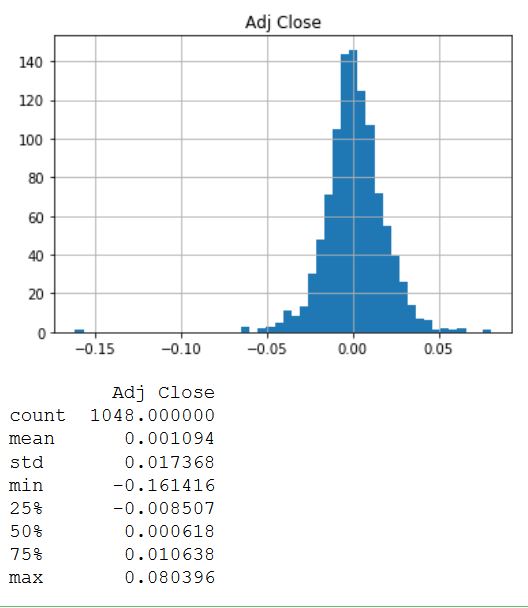
Распределение выглядит очень симметрично и нормально распределённым вокруг значения 0,00. Для получения других значений статистики используется функция description (). В результате видно, что среднее значение немного больше нуля, а стандартное отклонение составляет практически 0,02.

Кумулятивная доходность

Кумулятивная дневная прибыль полезна для определения стоимости инвестиций через определенные промежуток времени. Ее можно рассчитать, как приводится в коде ниже.

# Кумулютивная дневная доходность
cum_daily_return = (1 + daily_pct_change).cumprod()

print(cum_daily_return.tail())

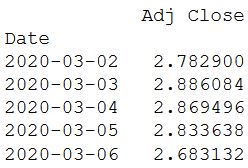
# Построение кумулятивной дневной доходности
cum_daily_return.plot(figsize=(12,8))

plt.show()

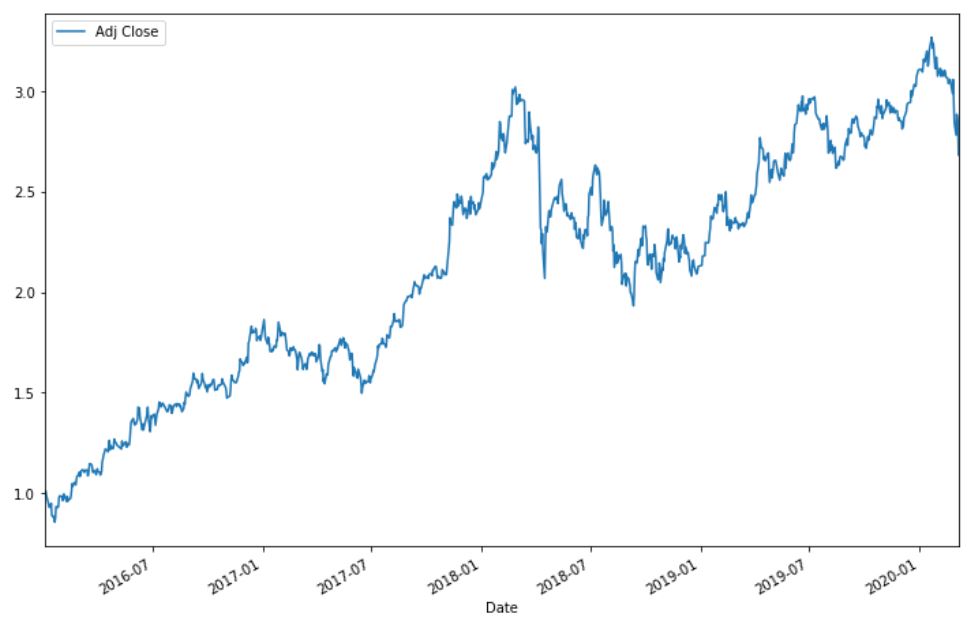
Можно пересчитать доходность в месячном периоде:

# Месячная кумулятивная доходность
cum_monthly_return = cum_daily_return.resample("M").mean()

print(cum_monthly_return.tail())

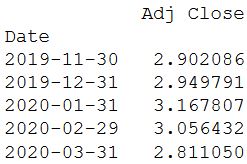
Знание того, как рассчитать доходность, является ценным при анализе акции. Но еще большую ценность оно представляет при сравнении с другими акциями.

Возьмем некоторые акции (выбор их совершенно случайный) и построим их диаграмму.

ticker = ['AFLT.ME','DSKY.ME','IRAO.ME','PIKK.ME', 'PLZL.ME','SBER.ME','ENRU.ME']

stock = yf.download(ticker,'2018-01-01')

# Дневная доходность в `daily_close_px`
daily_pct_change = stock['Adj Close'].pct_change()

# Распределение
daily_pct_change.hist(bins=50, sharex=True, figsize=(20,8))

plt.show()

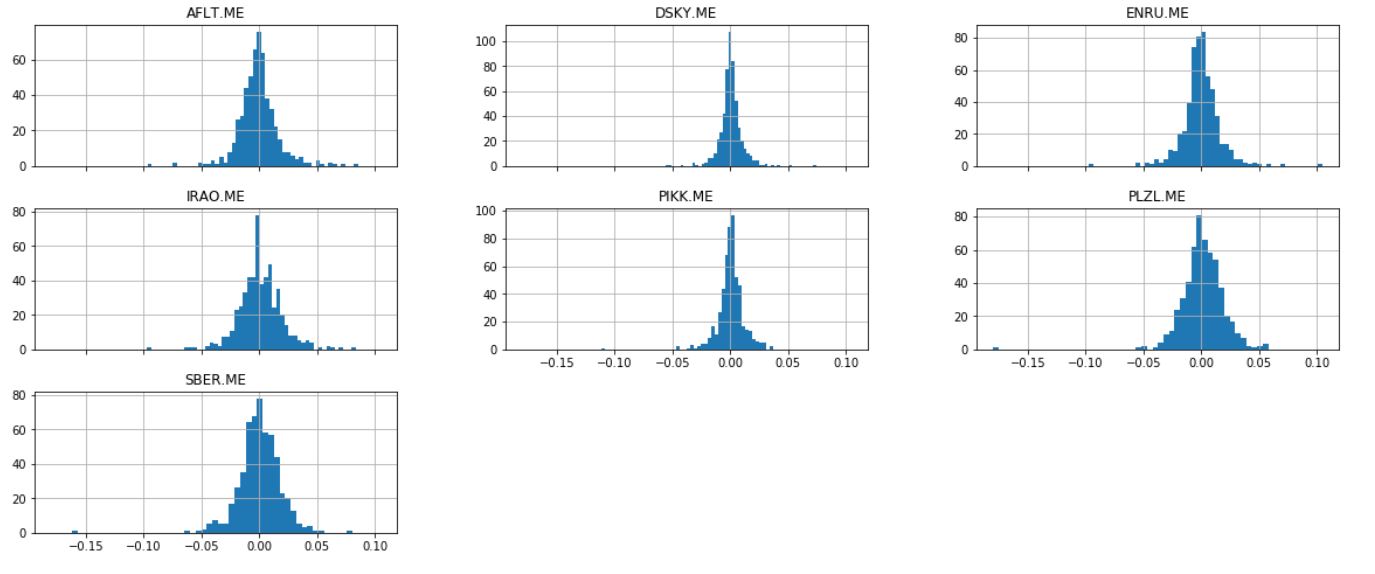
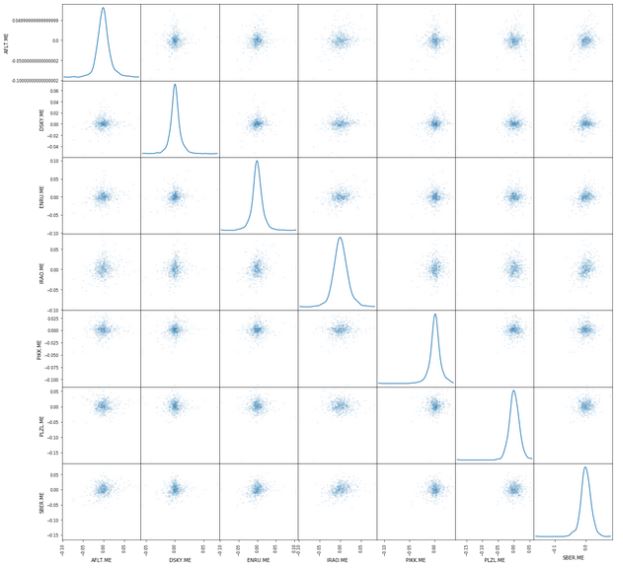
Еще один полезный график —матрица рассеяния. Ее можно легко построить при помощи функции scatter_matrix (), входящей в библиотеку pandas. В качестве аргументов используется daily_pct_change и устанавливается параметр Ядерной оценки плотности — Kernel Density Estimation. Кроме того, можно установить прозрачность с помощью параметра alpha и размер графика с помощью параметра figsize.

from pandas.plotting import scatter_matrix

# Матрица рассеивания `daily_pct_change`  
scatter_matrix(daily_pct_change, diagonal='kde', alpha=0.1,figsize=(20,20))

plt.show()

На этом пока все. В следующей статье будет рассмотрено вычисление волатильности, средней и использование метода наименьших квадратов.