
Итак, вашему вниманию представляется перевод страницы Time series forecasting из раздела руководств tensorflow: ссылка. Мои дополнения вместе с иллюстрациями к переводу нацелены помочь с пониманием основных идей в одном из самых интересных направлений ML и эконометрики в целом – прогнозировании временных рядов.
Небольшое вступление перед переводом.
Руководство представляет собой описание выполнения прогнозирования температуры воздуха на основе одномерных временных рядов (univariate time-series) и многомерных временных рядов (multivariate time-series). Для каждой части подаваемые на вход модели данные (input data) должны быть подготовлены соответствующим образом. С учётом рассматриваемого в данном руководстве набора метеорологических данных, разделение имеет следующий вид:
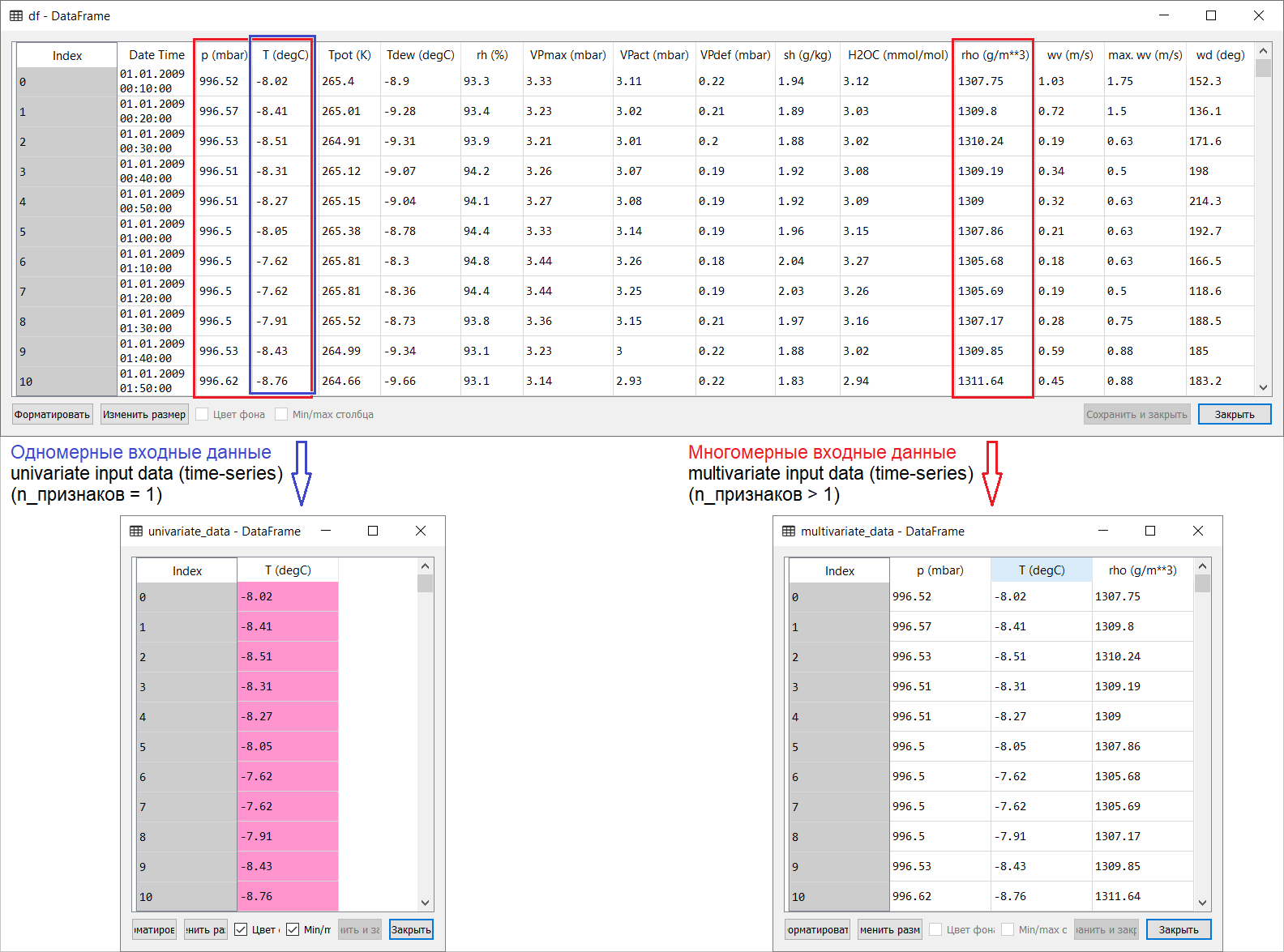
На вопросы о том, что брать за Х а что за Y, то есть как подготовить данные под класс контролируемого обучения, станет ясно из последующих иллюстраций. Отмечу только, что формирование целевого вектора (Y) для работы как с одномерным, так и многомерным временным рядом одинаковое: целевой вектор составляется на основе признака Т(degC) (температура воздуха). Разница между ними «зарыта» в формировании набора признаков, подающихся на вход модели: в случае с одномерным временным рядом для прогнозирования температуры в будущем входной вектор (X) состоит из одного признака: собственно, температуры воздуха; а для многомерного – более чем одного: помимо температуры воздуха в примере рассматриваемого руководства используются p(mbar) (атмосферное давление) и rho(g/m**3) (влажность).
На первый, далеко-поверхностный, взгляд пример с прогнозированием температуры выглядит неубедительно с точки зрения применения многомерного входа: для прогнозирования температуры наиболее релевантным признаком будет температура. Однако это совершенно не так: для выработки качественного прогноза температуры воздуха нужно учитывать множество факторов, вплоть до трения воздуха о земную поверхность и т.п. К тому же на практике некоторые вещи далеко не очевидны, да и целевой вектор может быть в виде той ещё солянки (или борща). В этой связи разведочный анализ данных с отбором наиболее релевантных признаков для последующего формирования многомерного входа является единственным правильным решением.
Итак, перевод руководства представлен ниже. Дополнительный текст будет выделен курсивом.
Прогнозирование временных рядов
Данное руководство представляет собой введение в прогнозирование временных рядов с использованием рекуррентных нейронных сетей (РНС, от англ. Recurrent Neural Network, RNN). Оно состоит из двух частей: в первой описывается прогнозирование температуры воздуха на основе одномерного временного ряда, во второй — на основе многомерного временного ряда.
import tensorflow as tf
import matplotlib as mpl
import matplotlib.pyplot as plt
import numpy as np
import os
import pandas as pd
mpl.rcParams['figure.figsize'] = (8, 6)
mpl.rcParams['axes.grid'] = False
Набор метеорологических данных
Во всех примерах руководства используются временные последовательности данных о погоде, записанные на гидрометеорологической станции в Институте биогеохимии им. Макса Планка.
В этот набор данных включены замеры 14 различных метеорологических показателей (таких, как температура воздуха, атмосферное давление, влажность), выполняющиеся каждые 10 минут начиная с 2003 года. Для экономии времени и используемой памяти в руководстве будут использоваться данные, охватывающие период с 2009 по 2016 год. Этот раздел набора данных был подготовлен Франсуа Шолле (François Chollet) для его книги «Глубокое обучение на Python» (Deep Learning with Python).
zip_path = tf.keras.utils.get_file(
origin='https://storage.googleapis.com/tensorflow/tf-keras-datasets/jena_climate_2009_2016.csv.zip',
fname='jena_climate_2009_2016.csv.zip',
extract=True)
csv_path, _ = os.path.splitext(zip_path)
df = pd.read_csv(csv_path)
Посмотрим, что у нас имеется.
df.head()

В том, что период записи наблюдения составляет 10 минут, можно убедиться по вышеприведённой таблице. Таким образом, в течение одного часа у вас будет 6 наблюдений. В свою очередь за сутки накапливается 144 (6×24) наблюдения.
Допустим, вы хотите cпрогнозировать температуру, которая будет через 6 часов в будущем. Этот прогноз вы делаете на основе имеющихся у вас данных за определённый период: например, вы решили использовать 5 дней наблюдений. Следовательно, для обучения модели вы должны создать временной интервал, содержащий последние 720 (5×144) наблюдений (в виду того, что возможны разные конфигурации, данный набор данных является хорошей основой для экспериментов).
Приведенная ниже функция возвращает вышеописанные временные интервалы для обучения модели. Аргумент history_size — это размер последнего временного интервала, target_size – аргумент, определяющий насколько далеко в будущее модель должна научиться прогнозировать. Другими словами, target_size – это целевой вектор, который необходимо спрогнозировать.
def univariate_data(dataset, start_index, end_index, history_size, target_size):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i)
# Reshape data from (history_size,) to (history_size, 1)
data.append(np.reshape(dataset[indices], (history_size, 1)))
labels.append(dataset[i+target_size])
return np.array(data), np.array(labels)
В обеих частях руководства первые 300 000 строк данных будут использоваться для обучения модели, оставшиеся – для её валидации (проверки). В этом случае объём обучающих данных составляет примерно 2100 дней.
TRAIN_SPLIT = 300000
Для обеспечения воспроизводимости результатов устанавливается функция seed.
tf.random.set_seed(13)
Часть 1. Прогнозирование на основе одномерного временного ряда
В первой части вы будете обучать модель, используя только один признак – температуру; обученная модель будет использоваться для прогнозирования будущих значений температуры.
Для начала извлечем только температуру из набора данных.
uni_data = df['T (degC)']
uni_data.index = df['Date Time']
uni_data.head()
Date Time
01.01.2009 00:10:00 -8.02
01.01.2009 00:20:00 -8.41
01.01.2009 00:30:00 -8.51
01.01.2009 00:40:00 -8.31
01.01.2009 00:50:00 -8.27
Name: T (degC), dtype: float64
И посмотрим, как эти данные изменяются во времени.
uni_data.plot(subplots=True)

uni_data = uni_data.values
Перед обучением искусственной нейронной сети (далее – ИНС) важным шагом является масштабирование данных. Одним из распространённых способов выполнения масштабирования является стандартизация (standardization), выполняемая путём вычитания среднего значения и деления на стандартное отклонение для каждого признака. Вы также можете использовать метод tf.keras.utils.normalize, который масштабирует значения в диапазон [0,1].
Примечание: стандартизация должна выполняться только c использованием обучающих данных.
uni_train_mean = uni_data[:TRAIN_SPLIT].mean()
uni_train_std = uni_data[:TRAIN_SPLIT].std()
Выполним стандартизацию данных.
uni_data = (uni_data-uni_train_mean)/uni_train_std
Далее подготовим данные для модели с одномерным входом. На вход в модель будут подаваться последние 20 зарегистрированных наблюдений за температурой, и модель необходимо обучить прогнозировать температуру на следующем шаге по времени.
univariate_past_history = 20
univariate_future_target = 0
x_train_uni, y_train_uni = univariate_data(uni_data, 0, TRAIN_SPLIT,
univariate_past_history,
univariate_future_target)
x_val_uni, y_val_uni = univariate_data(uni_data, TRAIN_SPLIT, None,
univariate_past_history,
univariate_future_target)
Результаты применения функции univariate_data.
print ('Single window of past history')
print (x_train_uni[0])
print ('n Target temperature to predict')
print (y_train_uni[0])
[-2.04513467]
[-2.08334362]
[-2.09723778]
[-2.09376424]
[-2.09144854]
[-2.07176515]
[-2.07176515]
[-2.07639653]
[-2.08913285]
[-2.09260639]
[-2.10418486]]
Target temperature to predict
-2.1041848598100876
Дополнение: подготовка данных для модели с одномерным входом схематично изображена на следующем рисунке (для удобства на этом и последующих рисунках данные представлены в «сыром» виде, до стандартизации, а также без признака ‘Date time’ в качестве индекса):

Теперь, когда данные соответствующим образом подготовлены, рассмотрим конкретный пример. Передаваемая в ИНС информация выделена синим цветом, красным крестиком обозначено будущее значение, которое ИНС должна спрогнозировать.
def create_time_steps(length):
return list(range(-length, 0))
def show_plot(plot_data, delta, title):
labels = ['History', 'True Future', 'Model Prediction']
marker = ['.-', 'rx', 'go']
time_steps = create_time_steps(plot_data[0].shape[0])
if delta:
future = delta
else:
future = 0
plt.title(title)
for i, x in enumerate(plot_data):
if i:
plt.plot(future, plot_data[i], marker[i], markersize=10,
label=labels[i])
else:
plt.plot(time_steps, plot_data[i].flatten(), marker[i], label=labels[i])
plt.legend()
plt.xlim([time_steps[0], (future+5)*2])
plt.xlabel('Time-Step')
return plt
show_plot([x_train_uni[0], y_train_uni[0]], 0, 'Sample Example')

Базовое решение (без привлечения машинного обучения)
Прежде чем приступить к обучению модели, установим простое базовое решение (baseline). Оно заключается в следующем: для заданного входного вектора метод базового решения «просматривает» всю историю и прогнозирует следующее значение как среднее из последних 20 наблюдений.
def baseline(history):
return np.mean(history)
show_plot([x_train_uni[0], y_train_uni[0], baseline(x_train_uni[0])], 0,
'Baseline Prediction Example')
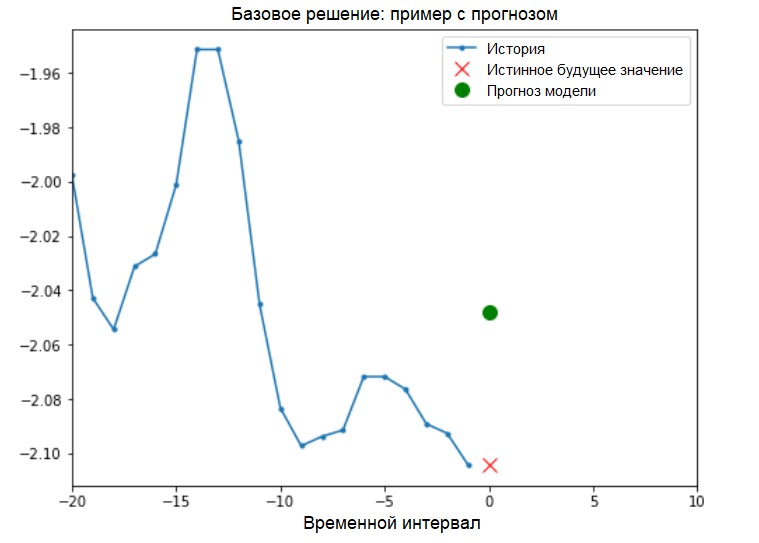
Посмотрим, сможем ли мы превзойти результат «усреднения», использую рекуррентную нейронную сеть.
Рекуррентная нейронная сеть
Рекуррентная нейронная сеть (РНС) — это тип ИНС, который хорошо подходит для решения задач, связанных с временными рядами. РНС шаг за шагом обрабатывает временную последовательность данных, перебирая её элементы и сохраняя внутреннее состояние, полученное при обработке предыдущих элементов. Более подробную информацию о РНС вы можете найти в следующем руководстве. В данном руководстве будет использоваться специализированный слой РНС, который называется «Долгая краткосрочная память» (англ. Long Short-Term Memory, LSTM).
Далее с помощью tf.data выполним перемешивание (shuffle), пакетирование (batch) и кэширование (cache) набора данных.
Дополнение:
Подробнее про методы shuffle, batch и cache на странице tensorflow:
BATCH_SIZE = 256
BUFFER_SIZE = 10000
train_univariate = tf.data.Dataset.from_tensor_slices((x_train_uni, y_train_uni))
train_univariate = train_univariate.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_univariate = tf.data.Dataset.from_tensor_slices((x_val_uni, y_val_uni))
val_univariate = val_univariate.batch(BATCH_SIZE).repeat()
Следующая визуализация должна помочь понять, как выглядят данные после пакетной обработки.

Видно, что LSTM требует определённой формы ввода данных, которые ему предоставляются.
simple_lstm_model = tf.keras.models.Sequential([
tf.keras.layers.LSTM(8, input_shape=x_train_uni.shape[-2:]),
tf.keras.layers.Dense(1)
])
simple_lstm_model.compile(optimizer='adam', loss='mae')
Проверим выход модели.
for x, y in val_univariate.take(1):
print(simple_lstm_model.predict(x).shape)
(256, 1)
Дополнение:
В общем плане РНС работают с последовательностями (sequences). Это означает, что подаваемые на вход модели данные должны иметь следующую форму:
[наблюдения, временной интервал, кол-во признаков]
Форма обучающих данных для модели с одномерным входом имеет следующий вид:
print(x_train_uni.shape)
(299980, 20, 1)
Далее займёмся обучением модели. Из-за большого размера набора данных и в целях экономии времени каждая эпоха будет проходить только 200 шагов (steps_per_epoch=200) вместо полных данных обучения, как это обычно делается.
EVALUATION_INTERVAL = 200
EPOCHS = 10
simple_lstm_model.fit(train_univariate, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_univariate, validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 2s 11ms/step - loss: 0.4075 - val_loss: 0.1351
Epoch 2/10
200/200 [==============================] - 1s 4ms/step - loss: 0.1118 - val_loss: 0.0360
Epoch 3/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0490 - val_loss: 0.0289
Epoch 4/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0444 - val_loss: 0.0257
Epoch 5/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0299 - val_loss: 0.0235
Epoch 6/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0317 - val_loss: 0.0224
Epoch 7/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0287 - val_loss: 0.0206
Epoch 8/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0263 - val_loss: 0.0200
Epoch 9/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0254 - val_loss: 0.0182
Epoch 10/10
200/200 [==============================] - 1s 4ms/step - loss: 0.0228 - val_loss: 0.0174
Прогнозирование с использованием простой модели LSTM
После выполнения подготовки простой LSTM-модели, выполним несколько прогнозов.
for x, y in val_univariate.take(3):
plot = show_plot([x[0].numpy(), y[0].numpy(),
simple_lstm_model.predict(x)[0]], 0, 'Simple LSTM model')
plot.show()

Выглядит лучше, чем базовый уровень.
Теперь, когда вы ознакомились с основами, давайте перейдем ко второй части, в которой описывается работа с многомерным временным рядом.
Часть 2: Прогнозирование на основе многомерного временного ряда
Как было сказано, исходный набор данных содержит 14 различных метеорологических показателей. Для простоты и удобства во второй части рассматриваются только три из них — температура воздуха, атмосферное давление и плотность воздуха.
Чтобы использовать больше признаков, их названия нужно добавить в список feature_considered.
features_considered = ['p (mbar)', 'T (degC)', 'rho (g/m**3)']
features = df[features_considered]
features.index = df['Date Time']
features.head()
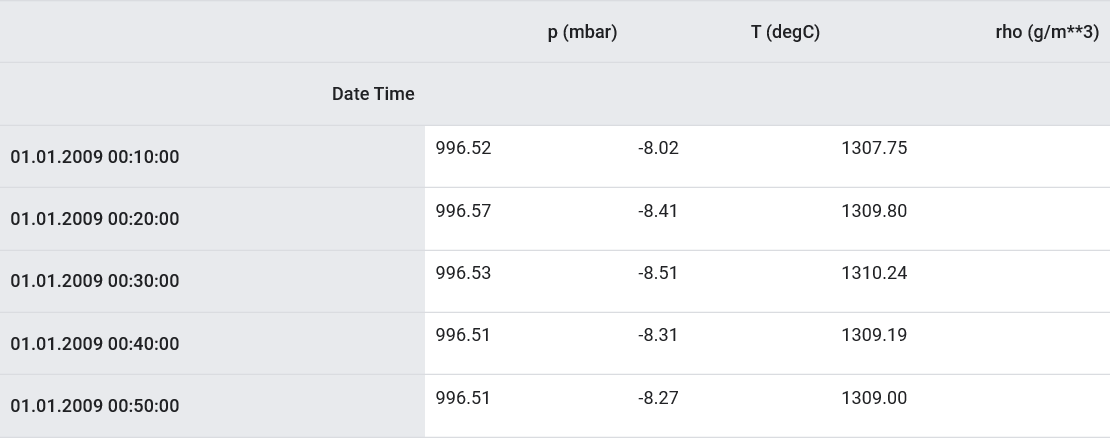
Посмотрим, как эти показатели изменяются во времени.
features.plot(subplots=True)
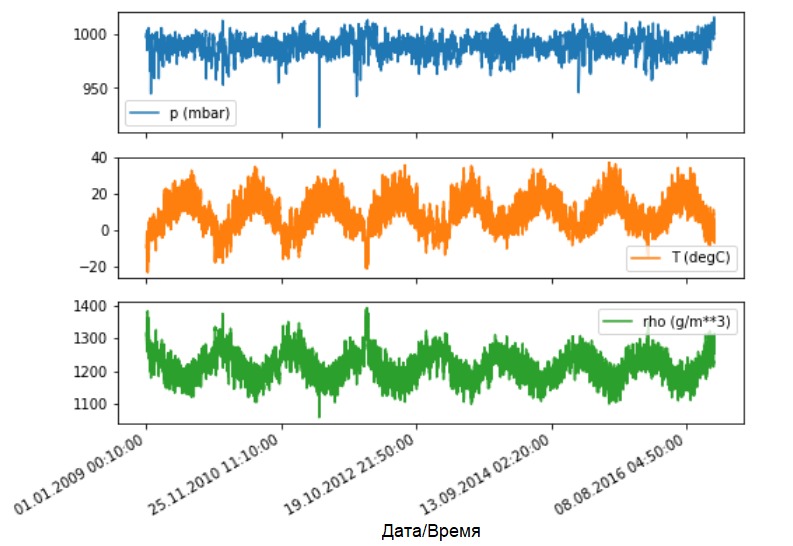
Как и ранее, первым шагом будет выполнение стандартизации набора данных с вычислением среднего значения и стандартного отклонения обучающих данных.
dataset = features.values
data_mean = dataset[:TRAIN_SPLIT].mean(axis=0)
data_std = dataset[:TRAIN_SPLIT].std(axis=0)
dataset = (dataset-data_mean)/data_std
Дополнение:
Далее в руководстве будет рассказано о точечном и интервальном прогнозировании.
Суть в следующем. Если вам нужно, чтобы модель прогнозировала одно значение в будущем (например, значение температуры через 12 часов) (one-step/single step model), то и обучить модель вы должны таким образом, чтобы она прогнозировала только одно значение в будущем. Если задача состоит в прогнозировании интервала значений в будущем (например, ежечасные значения температуры в течение следующих 12 часов) (multi-step model), то и модель должна быть обучена прогнозировать интервал значений в будущем.

Точечное прогнозирование
В данном случае модель обучается прогнозированию одного значения в будущем на основе некой имеющейся истории.
Приведенная ниже функция выполняет ту же задачу организации временных интервалов лишь с тем отличием, что здесь она отбирает последние наблюдения на основе заданного размера шага.
def multivariate_data(dataset, target, start_index, end_index, history_size,
target_size, step, single_step=False):
data = []
labels = []
start_index = start_index + history_size
if end_index is None:
end_index = len(dataset) - target_size
for i in range(start_index, end_index):
indices = range(i-history_size, i, step)
data.append(dataset[indices])
if single_step:
labels.append(target[i+target_size])
else:
labels.append(target[i:i+target_size])
return np.array(data), np.array(labels)
В данном руководстве ИНС оперирует данными за последние пять (5) дней, то есть 720 наблюдениями (6х24х5). Допустим, что отбор данных проводится не каждые 10 минут, а каждый час: в течение 60 минут резкие изменения не ожидаются. Следовательно, историю последних пяти дней составляют 120 наблюдений (720/6). Для модели, выполняющей точечное прогнозирование, целью является значение температуры через 12 часов в будущем. В этом случае целевой вектор будет составлять температура после 72 (12х6) наблюдений (см. следующее дополнение. – Прим. переводчика).
past_history = 720
future_target = 72
STEP = 6
x_train_single, y_train_single = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP,
single_step=True)
x_val_single, y_val_single = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP,
single_step=True)
Проверим временной интервал.
print ('Single window of past history : {}'.format(x_train_single[0].shape))
Single window of past history : (120, 3)
train_data_single = tf.data.Dataset.from_tensor_slices((x_train_single, y_train_single))
train_data_single = train_data_single.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_single = tf.data.Dataset.from_tensor_slices((x_val_single, y_val_single))
val_data_single = val_data_single.batch(BATCH_SIZE).repeat()
single_step_model = tf.keras.models.Sequential()
single_step_model.add(tf.keras.layers.LSTM(32,
input_shape=x_train_single.shape[-2:]))
single_step_model.add(tf.keras.layers.Dense(1))
single_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(), loss='mae')
Проверим нашу выборку и выведем кривые потерь на этапах обучения и проверки.
for x, y in val_data_single.take(1):
print(single_step_model.predict(x).shape)
(256, 1)
single_step_history = single_step_model.fit(train_data_single, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_single,
validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 4s 18ms/step - loss: 0.3090 - val_loss: 0.2646
Epoch 2/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2624 - val_loss: 0.2435
Epoch 3/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2616 - val_loss: 0.2472
Epoch 4/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2567 - val_loss: 0.2442
Epoch 5/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2263 - val_loss: 0.2346
Epoch 6/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2416 - val_loss: 0.2643
Epoch 7/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2411 - val_loss: 0.2577
Epoch 8/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2410 - val_loss: 0.2388
Epoch 9/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2447 - val_loss: 0.2485
Epoch 10/10
200/200 [==============================] - 2s 9ms/step - loss: 0.2388 - val_loss: 0.2422
def plot_train_history(history, title):
loss = history.history['loss']
val_loss = history.history['val_loss']
epochs = range(len(loss))
plt.figure()
plt.plot(epochs, loss, 'b', label='Training loss')
plt.plot(epochs, val_loss, 'r', label='Validation loss')
plt.title(title)
plt.legend()
plt.show()
plot_train_history(single_step_history,
'Single Step Training and validation loss')
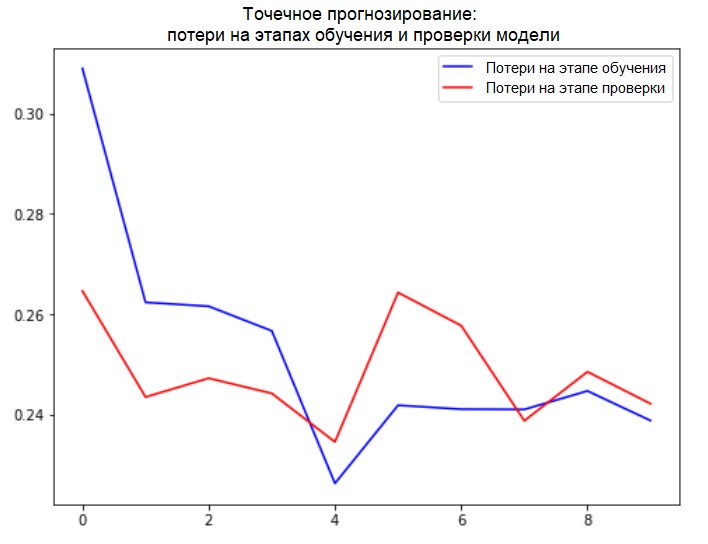
Дополнение:
Подготовка данных для модели с многомерным входом, выполняющей точечное прогнозирование, схематично изображена на следующем рисунке. Для удобства и более наглядного представления подготовки данных аргумент STEP равен 1. Обратите внимание, что в приводимых функциях-генераторах аргумент STEP предназначен только для формирования истории, а не для целевого вектора.
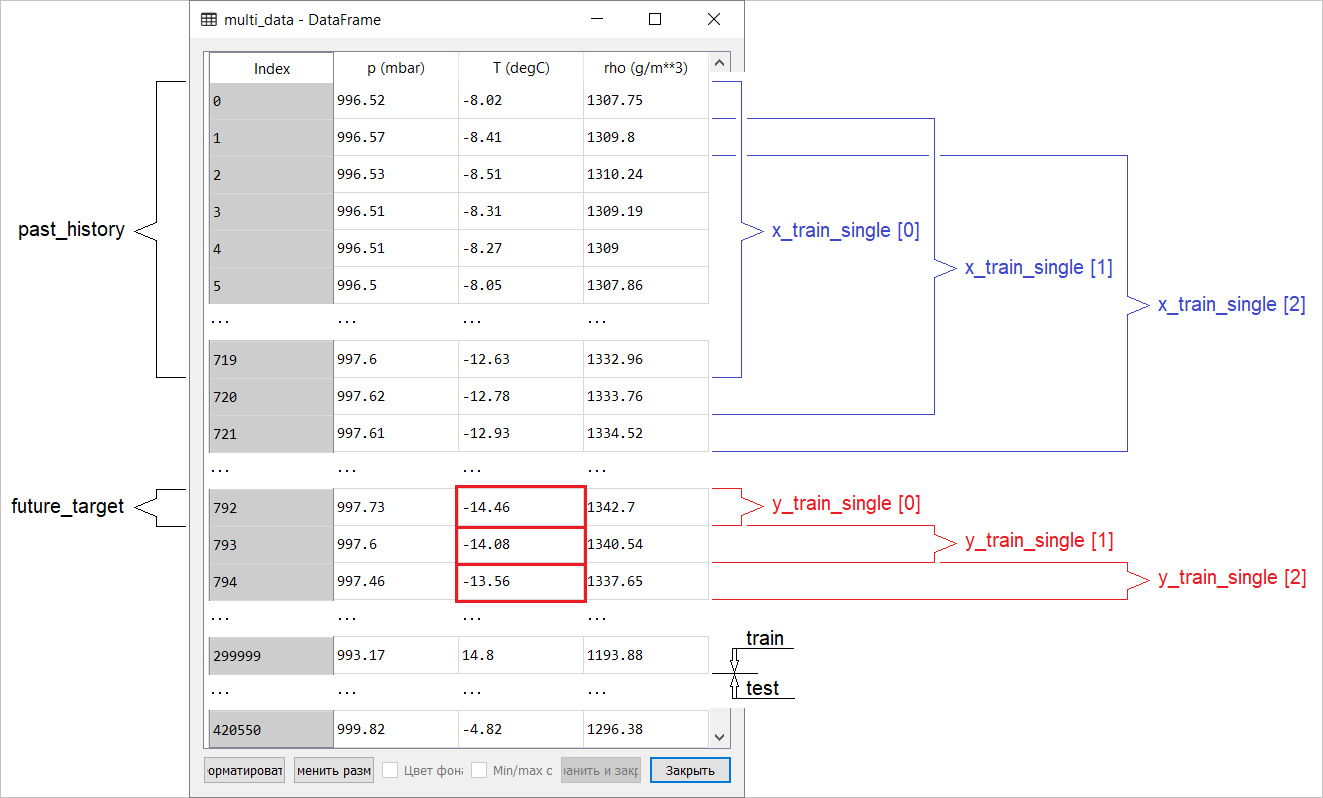
В этом случае x_train_single имеет форму (299280, 720, 3).
При STEP=6, форма примет следующий вид: (299280, 120, 3) и скорость выполнения функции увеличиться в разы. Вообще нужно отдать должное программисту: представленные в руководстве генераторы очень прожорливые в плане потребляемой памяти.
Выполнение точечного прогноза
Теперь, когда модель обучена, выполним несколько пробных прогнозов. На вход модели подаётся история наблюдений 3-х признаков за последние пять дней, отобранных каждый час (временной интервал = 120). Так как наша цель заключается в прогнозе только температуры, то синим цветом на графике отображены прошлые значения температуры (история). Прогноз выполнен на полдня в будущее (отсюда и разрыв между историей и спрогнозированным значением).
for x, y in val_data_single.take(3):
plot = show_plot([x[0][:, 1].numpy(), y[0].numpy(),
single_step_model.predict(x)[0]], 12,
'Single Step Prediction')
plot.show()

Интервальное прогнозирование
В этом случае на основе некой имеющейся истории модель обучается прогнозированию интервала будущих значений. Таким образом, в отличие модели, прогнозирующей только на одно значение в будущее, данная модель прогнозирует последовательность значений в будущем.
Допустим, как и в случае с моделью, выполняющей точечное прогнозирование, для модели, выполняющей интервальное прогнозирование, обучающими данными являются почасовые замеры последних пяти дней (720/6). Однако в данном случае модель необходимо обучить прогнозировать температуру на следующие 12 часов. Поскольку наблюдения регистрируются каждые 10 минут, выход (output) модели должен состоять из 72 прогнозов. Для выполнения этой задачи необходимо подготовить набор данных заново, но с другим целевым интервалом.
future_target = 72
x_train_multi, y_train_multi = multivariate_data(dataset, dataset[:, 1], 0,
TRAIN_SPLIT, past_history,
future_target, STEP)
x_val_multi, y_val_multi = multivariate_data(dataset, dataset[:, 1],
TRAIN_SPLIT, None, past_history,
future_target, STEP)
Проверим выборку.
print ('Single window of past history : {}'.format(x_train_multi[0].shape))
print ('n Target temperature to predict : {}'.format(y_train_multi[0].shape))
Single window of past history : (120, 3)
Target temperature to predict : (72,)
train_data_multi = tf.data.Dataset.from_tensor_slices((x_train_multi, y_train_multi))
train_data_multi = train_data_multi.cache().shuffle(BUFFER_SIZE).batch(BATCH_SIZE).repeat()
val_data_multi = tf.data.Dataset.from_tensor_slices((x_val_multi, y_val_multi))
val_data_multi = val_data_multi.batch(BATCH_SIZE).repeat()
Дополнение: отличие в формировании целевого вектора для «интервальной модели» от «точечной модели» видно на следующем рисунке.

Подготовим визуализацию.
def multi_step_plot(history, true_future, prediction):
plt.figure(figsize=(12, 6))
num_in = create_time_steps(len(history))
num_out = len(true_future)
plt.plot(num_in, np.array(history[:, 1]), label='History')
plt.plot(np.arange(num_out)/STEP, np.array(true_future), 'bo',
label='True Future')
if prediction.any():
plt.plot(np.arange(num_out)/STEP, np.array(prediction), 'ro',
label='Predicted Future')
plt.legend(loc='upper left')
plt.show()
На этом и последующих аналогичных графиках история и будущие данные ежечасные.
for x, y in train_data_multi.take(1):
multi_step_plot(x[0], y[0], np.array([0]))
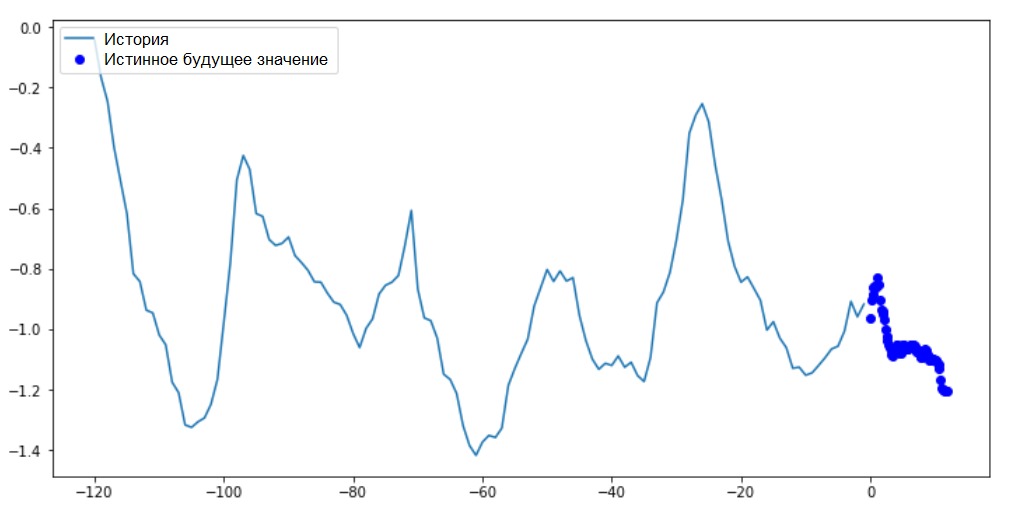
Так как эта задача немного сложнее, чем предыдущая, то модель будет состоять из двух слоёв LSTM. Наконец, поскольку выполняется 72 прогноза, выход слой насчитывает 72 нейрона.
multi_step_model = tf.keras.models.Sequential()
multi_step_model.add(tf.keras.layers.LSTM(32,
return_sequences=True,
input_shape=x_train_multi.shape[-2:]))
multi_step_model.add(tf.keras.layers.LSTM(16, activation='relu'))
multi_step_model.add(tf.keras.layers.Dense(72))
multi_step_model.compile(optimizer=tf.keras.optimizers.RMSprop(clipvalue=1.0), loss='mae')
Проверим нашу выборку и выведем кривые потерь на этапах обучения и проверки.
for x, y in val_data_multi.take(1):
print (multi_step_model.predict(x).shape)
(256, 72)
multi_step_history = multi_step_model.fit(train_data_multi, epochs=EPOCHS,
steps_per_epoch=EVALUATION_INTERVAL,
validation_data=val_data_multi,
validation_steps=50)
Train for 200 steps, validate for 50 steps
Epoch 1/10
200/200 [==============================] - 21s 103ms/step - loss: 0.4952 - val_loss: 0.3008
Epoch 2/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3474 - val_loss: 0.2898
Epoch 3/10
200/200 [==============================] - 18s 89ms/step - loss: 0.3325 - val_loss: 0.2541
Epoch 4/10
200/200 [==============================] - 18s 89ms/step - loss: 0.2425 - val_loss: 0.2066
Epoch 5/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1963 - val_loss: 0.1995
Epoch 6/10
200/200 [==============================] - 18s 90ms/step - loss: 0.2056 - val_loss: 0.2119
Epoch 7/10
200/200 [==============================] - 18s 91ms/step - loss: 0.1978 - val_loss: 0.2079
Epoch 8/10
200/200 [==============================] - 18s 89ms/step - loss: 0.1957 - val_loss: 0.2033
Epoch 9/10
200/200 [==============================] - 18s 90ms/step - loss: 0.1977 - val_loss: 0.1860
Epoch 10/10
200/200 [==============================] - 18s 88ms/step - loss: 0.1904 - val_loss: 0.1863
plot_train_history(multi_step_history, 'Multi-Step Training and validation loss')

Выполнение интервального прогноза
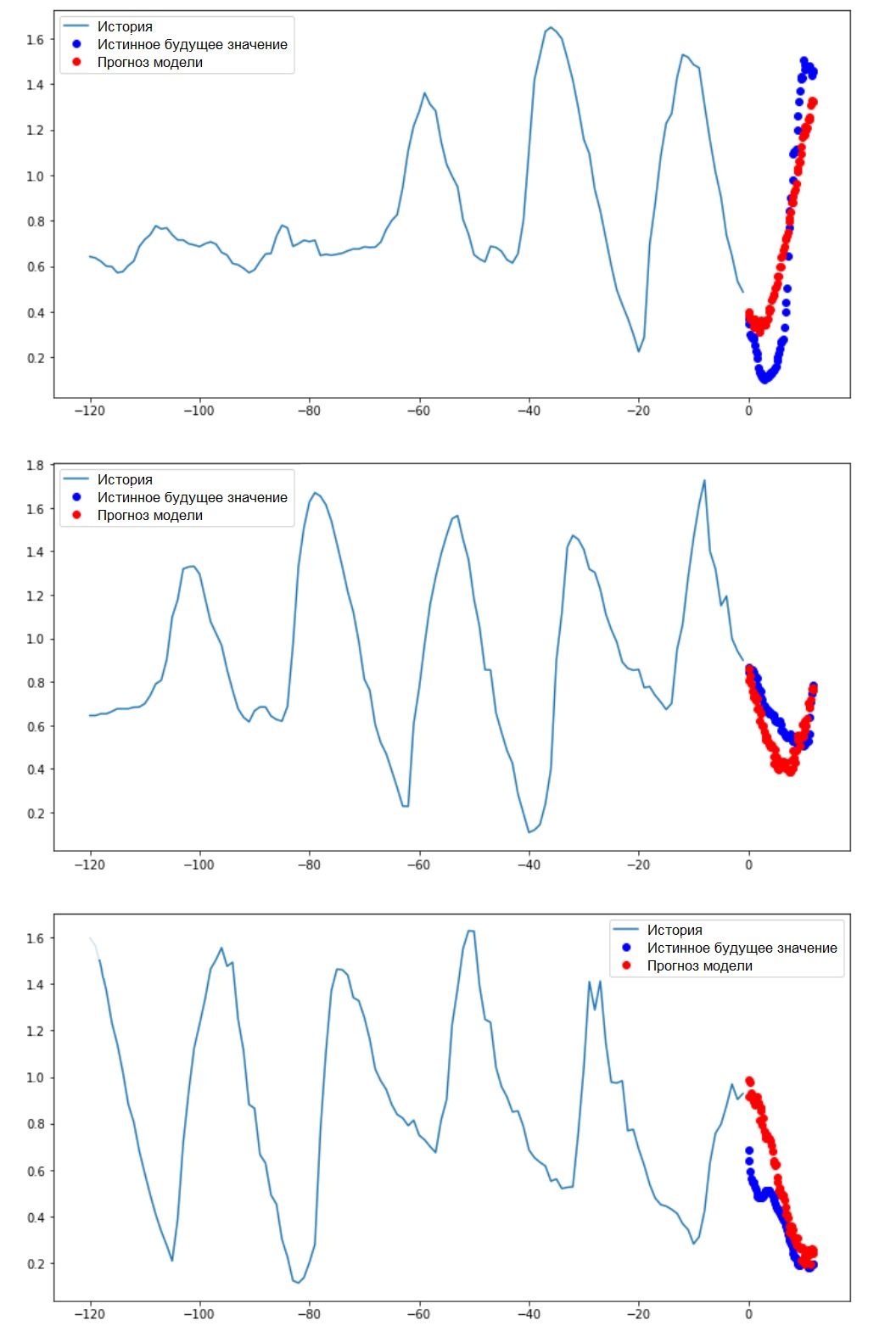
Итак, давайте выясним, насколько успешно обученная ИНС справляется с прогнозами будущих значений температуры.
for x, y in val_data_multi.take(3):
multi_step_plot(x[0], y[0], multi_step_model.predict(x)[0])
Следующие шаги
Данное руководство представляет собой краткое введение в прогнозирование временных рядов с использованием РНС. Теперь вы можете попытаться предсказать фондовый рынок и стать миллиардером (в оригинале именно так:). – Прим. переводчика).
Кроме того, вы можете написать собственный генератор для подготовки данных вместо функции uni/multivariate_data с целью более эффективного использования памяти. Также вы можете ознакомиться с работой «time series windowing» и привнести её идеи в данное руководство.
Для дальнейшего понимания рекомендуется прочесть главу 15 книги «Прикладное машинное обучение с помощью Scikit-Learn, Keras и TensorFlow» (Орельен Жерон, 2-е издание) и главу 6 книги «Глубокое обучение на Python» (Франсуа Шолле).
Заключительное дополнение
Оставаясь дома, позаботьтесь не только о своём здоровье, но и пожалейте компьютер путём выполнения примеров руководства на усечённом наборе данных. Например, с учётом пропорции 70х30 (тренировка/проверка), можно ограничить его следующим образом:
dataset = features[300000:].values
TRAIN_SPLIT = 85000Специально для сайта ITWORLD.UZ. Новость взята с сайта Хабр
