
При первом знакомстве с концепцией рекурсии, она может показаться странной и отталкивающей. Это кажется почти парадоксальным: как мы можем найти решение проблемы, используя решение той же проблемы? Несмотря на это, в большинстве проектов, рекурсию используют в программировании уже на ранних стадиях производства.
 От рекурсии может заболеть голова
От рекурсии может заболеть головаЯ думаю, что тем, кто пытается постигнуть концепцию рекурсии, следует сначала понять, что рекурсия — это больше, чем просто практика в программировании. Это философия решения проблем, которые можно решать частями, не трогая основную часть проблемы, при этом, проблема упрощается или становится меньше. Рекурсия применима не только в программировании, но и в простых повседневных задачах. Например, возьмите меня, пишущего эту статью: допустим, я хочу написать около 1000 слов, и ставлю цель писать 100 слов каждый раз, когда сажусь за работу. Получается, что в первый раз я напишу 100 слов и оставляю 900 слов на потом. В следующий раз я напишу ещё 100 слов, а оставлю 800. Я буду продолжать, пока не останется 0 слов. Каждый раз, я частично решаю проблему, а оставшаяся часть проблемы уменьшается.
Работу над статьей можно представить в виде такого кода:
write_words(words_left):
if words left > 0:
write_100_words()
words_left = words_left - 100
write_words(words_left)
Также, этот алгоритм можно реализовать итеративно:
write_words(words_left):
while words_left > 0:
write_100_words()
words_left = words_left - 100
Если рассматривать вызов функции write_words(1000) в любой из этих реализаций, вы обнаружите, одинаковое поведение. На самом деле, каждую задачу, которую можно решить с помощью рекурсии, мы также можем решить с помощью итерации (циклы forи while). Так почему же стоит использовать именно рекурсию?
 Я пишу статью рекурсивно
Я пишу статью рекурсивноПочему рекурсия?
Хотите верьте, хотите нет, но с помощью рекурсии некоторые проблемы решить легче, чем с помощью итерации. Иногда рекурсия более эффективна, иногда более читаема, а иногда просто быстрее реализуется. Некоторые структуры данных, такие как деревья ― хорошо подходят для рекурсивных алгоритмов. Существуют языки программирования, в которых вообще нет понятия цикла — это чисто функциональные языки, такие как Haskell, они полностью зависят от рекурсии для итеративного решения задач. Я хочу сказать, что программисту не обязательно понимать рекурсию, но хороший программист, просто обязан в этом разбираться. Более того, понимание рекурсии сделает вас отличным «решателем» проблем, не только в программировании!
Суть рекурсии
В общем, рекурсивный подход подразумевает разделение сложной задачи, на один простой шаг к её решению и оставшуюся часть, которая становится упрощённой версией той же задачи. Затем этот процесс повторяется. Каждый раз вы совершаете один шаг, до тех пор, пока задача упростится до одного простейшего решения (его называют «базовым случаем»). Простейшее решение нашего базового случая с шагами, которые мы предприняли, чтобы добраться до него, образуют решение нашей первоначальной задачи.
 Мы каждый раз разделяем задачу «P» на шаги и оставшуюся упрощённую задачу той же формы, что и оригинал, пока не достигнем простого решения небольшой проблемы (базовый случай).
Мы каждый раз разделяем задачу «P» на шаги и оставшуюся упрощённую задачу той же формы, что и оригинал, пока не достигнем простого решения небольшой проблемы (базовый случай).Предположим, у нас есть фактические данные определённого типа, назовём их dₒ. Идея рекурсии состоит в том, чтобы предположить, что мы уже решили задачу или вычислили желаемую функцию f для всех форм этого типа данных. Каждая из этих форм проще общей сложности dₒ, которую нам нужно определить. Следовательно, если мы можем найти способ выражения f(dₒ), исходя из одной или нескольких частей f(d), где все эти d проще, чем dₒ, значит мы нашли решение для f(dₒ). Мы повторяем этот процесс, и рассчитываем, что в какой-то момент оставшиеся f(d) станут настолько простыми, что мы сможем легко реализовать фиксированное, окончательное решение для них. В итоге, решением исходной задачи станет поэтапное решение более простых задач.
В приведённом выше примере (про написание статьи), данными является текст, содержащийся в документе, который я должен написать, а степень сложности — это длина документа. Это немного надуманный пример, но если предположить, что я уже решил задачу f(900) (написать 900 слов), то все, что мне нужно сделать, чтобы решить f(1000), ― это написать 100 слов и выполнить решение для 900 слов, f(900).
Давайте рассмотрим пример получше: с числами Фибоначчи, где 1-е число равно 0, второе равно 1, а nᵗʰ число равно сумме двух предыдущих. Предположим, у нас есть функция Фибоначчи, которая сообщает нам nᵗʰ число:
fib(n):
if n == 0:
return 0
if n == 1:
return 1
else:
return fib(n-1) + fib(n-2)
Как будет выглядеть выполнение такой функции? Возьмём для примера fib(4):
 Визуализация древа рекурсии, показывающая рекурсивное вычисление, которое приводит к fib(4) = 3. Обратите внимание, что вычисление сначала выполняется в глубину.
Визуализация древа рекурсии, показывающая рекурсивное вычисление, которое приводит к fib(4) = 3. Обратите внимание, что вычисление сначала выполняется в глубину.В процессе рекурсивного решения задачи полезно повторять мантру: «Притворяйся, пока это не станет правдой», то есть делай вид, что ты уже решил более простую часть задачи. Затем попытайся уменьшить большую часть задачи, чтобы использовать решение упрощённой части. Подходящая для рекурсии задача, на самом деле должна иметь небольшое количество простых частей, которые нужно решить явно. Другими словами, метод сокращения до более простой задачи может быть использован для решения любого другого случая. Это можно проиллюстрировать на примере чисел Фибоначчи, где для определения fib(n) мы действуем, как будто мы уже рассчитали fib(n-1) и fib(n-2). В тоже время мы рассчитываем, что эти каскады и упрощения приведут к более простым случаям, пока мы не достигнем fib(0) и fib(1), которые имеют фиксированные и простые решения.
 «Притворяйся, пока это не станет правдой»
«Притворяйся, пока это не станет правдой»Рекурсивная стратегия
Рекурсивный подход — дело тонкое, и зависит от того, какую проблему вы пытаетесь решить. Тем не менее, есть некоторая общая стратегия, которая поможет вам двигаться в правильном направлении. Эта стратегия состоит из трёх шагов:
- Упорядочить данные
- Решить малую часть проблемы
- Решить большую часть проблемы
Как я уже говорил, я думаю, что для обучения полезно приводить пример, но помните, что рекурсивный подход зависит от конкретной задачи. Поэтому старайтесь сосредоточиться на общих принципах. Мы рассмотрим простой пример с реверсом строки. Мы напишем функцию reverse,которая будет работать так: reverse(‘Hello world’) = ‘dlrow olleH’. Я рекомендую вернуться назад и посмотреть, как эти шаги применяются к функции Фибоначчи, а затем попробовать применить их на других примерах (в интернете можно найти много упражнений).
Упорядочивание данных
Этот шаг является ключевым для решения проблем рекурсивным способом, и все же его часто упускают из виду или выполняют неявно. Какие бы данные мы ни использовали, будь то числа, строки, списки, бинарные древа или люди, необходимо явно найти целесообразный порядок, который даст нам видение, как упростить задачу. Порядок полностью зависит от конкретной задачи, но для начала стоит подумать об очевидных вариантах. Например: числа можно упорядочить по величине, строки и списки можно упорядочить по длине, бинарные древа по глубине, а люди могут быть упорядочены бесконечным количеством разумных способов: рост, вес или должность в организации. Это упорядочивание должно соответствовать степени сложности задачи, которую мы пытаемся решить.
 По порядку рассчитайсь, йехуу!
По порядку рассчитайсь, йехуу!После того, как мы упорядочили данные, нам нужно подумать об этом, как о чём-то, что мы можем сократить. На самом деле, мы можем записать наш порядок в виде последовательности:
0, 1, 2, …, n для чисел (т.е. для int данных d, степень(d) = d)
[], [■], [■, ■], …, [■, … , ■] для списков (len = 0, len = 1, …, len = n и т.д. для списка d, степень(d) = len(d))
Двигаясь справа налево, мы идём от общего («большая часть задачи») случая, к базовым («маленьким частям») случаям. В нашем примере с функцией reverse мы работаем со строкой, и можем взять длину строки за основу, для упорядочивания или определения степени сложности задачи.
Решаем малую часть проблемы
Как правило это самая лёгкая часть. После того, как мы определились с порядком, мы должны выделить в нём самые маленькие элементы, и решить, как мы будем обрабатывать их. Обычно, можно найти очевидное решение: в случае reverse(s), как только мы дойдём до len(s) == 0, имея при этом reverse(»), это будет знаком, что мы нашли ответ, потому что реверс пустой строки ничего не даст, т.е. нам вернётся пустая строка, так как у нас нет символов, которые можно перемещать. Если мы знаем решение для базового случая, и мы знаем порядок, то для нас, степень сложности решения общего случая, уменьшается в зависимости от степени сложности данных, которыми мы оперируем, приближаясь к базовым случаям. Мы должны быть внимательны, чтобы не пропустить ни одного базового случая: они и называются базовыми, потому что образуют основу порядка. Пропуск маленького шага считается распространённой ошибкой в сложных рекурсивных задачах, и приводит к бессмысленным данным или ошибкам.
Переходим к общим случаям
На этом этапе мы обрабатываем данные двигаясь вправо, то есть в сторону высокой степени. Как правило, мы рассматриваем данные произвольной степени, и ищем способ решения проблемы, упрощая её до выражения, представляющего ту же проблему, но в меньшей степени. Например, в случае с числами Фибоначчи мы начали с произвольного значения n и упростили fib(n) до fib(n-1) + fib(n-2), что является выражением, содержащим два экземпляра той же задачи, но в меньшей степени (n-1 и n-2, соответственно).
 Большой случай?
Большой случай?Возвращаясь к алгоритму reverse, мы можем рассмотреть произвольную строку с длинной n, и предположить, что наша reverseфункция работает для всех строк с длинной меньше n. Как мы можем использовать это, решая задачу для строки с длинной n? Мы могли бы сделать реверс строки, переместив всё, кроме последнего символа, а затем вставить этот последний символ в начало. В коде:
reverse(string) = reverse(string[-1]) + reverse(string[:-1])
где string[-1] соответствует последнему символу, а string[:-1]соответствует строке без последнего символа (это питонизм). Последний член функции reverse(string[:-1]), и является нашей исходной задачей, но он оперирует со строкой длины n-1. Таким образом, мы выразили нашу исходную задачу в решении той же задачи, но в уменьшенной степени.
Применив это решение к функции reverse, мы получаем следующее:
reverse(string):
if len(string) == 0:
return ''
else:
return string[-1] + reverse(string[:-1])
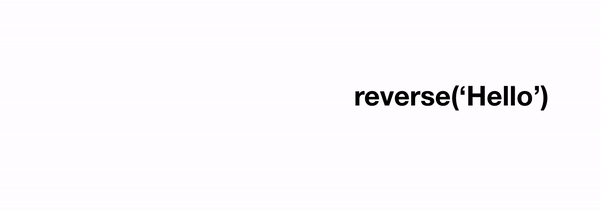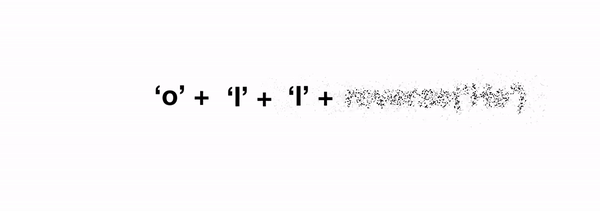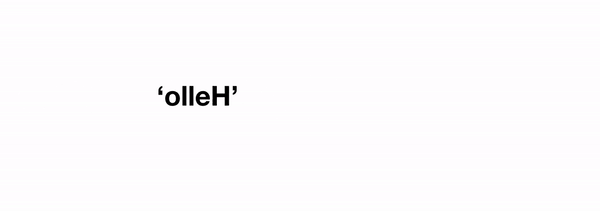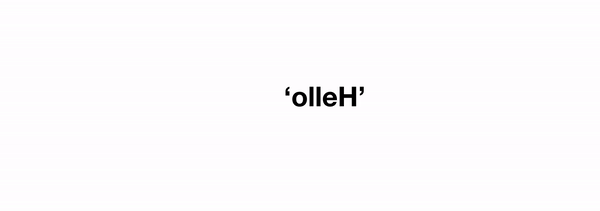 Визуализации рекурсивной функции reverse
Визуализации рекурсивной функции reverseЧасто бывает так, что нам нужно рассмотреть несколько рекурсивных случаев, так как данные определённого типа, могут принимать разные формы, но это полностью зависит от задачи. Например, если мы хотим сгладить список элементов, некоторые из которых сами могут быть списками, нам нужно будет различать случаи, когда элемент, который мы вытаскиваем из списка, является отдельным элементом или подсписком, что приводит по крайней мере к двум рекурсивным случаям.
Напутствие
Единственный способ улучшить свои навыки в рекурсии — это практика. В интернете можно найти тысяч примеров задач, подходящих для рекурсивного решения — испытайте себя. Однажды, вы неизбежно научитесь рекурсии, но, если у вас возникнут трудности с рекурсивным решением проблемы, попробуйте вместо этого итерацию. Рекурсия поможет вам решать проблемы не только в программировании, но и в повседневной жизни. Если проблема не подходит для рекурсии, что ж, такое бывает; со временем вы научитесь чувствовать, где следует использовать рекурсивный подход, а где итеративный.
Иногда в более сложных рекурсивных задачах, шаги 2 и 3, о которых мы говорили, принимают форму более циклического процесса. Если вы не можете быстро найти общее решение проблемы, попробуйте решить рекурсивные (большие) случаи и базовые (маленькие) случаи, которые сможете найти, а затем посмотрите, как в результате разделились разные части данных. Это должно выявить любые недостающие базовые и рекурсивные случаи или те, которые плохо взаимодействуют друг с другом и нуждаются в переосмыслении.
Наконец, помните, что выявление порядка является самым важным шагом к решению рекурсивной задачи, и ваша цель рассмотреть как правый (рекурсивный), так и левый (базовый) случаи этого порядка, чтобы решить задачу для всех данных определённого типа.

На этом всё, спасибо за внимание.
Специально для сайта ITWORLD.UZ. Новость взята с сайта NOP::Nuances of programming
