
Здесь можно посмотреть полный код.
Для того, чтобы полностью понять статью, нужны базовые знания принципов работы с numpy, линейной алгебры, работы с матрицами, дифференциации и метода градиентного спуска.
И прямо сейчас мы погрузимся в создание поверхностной модели нейронной сети. Для начала, загрузим наши данные.
import numpy as np
import matplotlib.pyplot as plt
import h5py
def load_data():
train_dataset = h5py.File('./train_catvnoncat.h5', "r")
train_set_x_orig = np.array(train_dataset["train_set_x"][:]) # признаки тренировочных данных
train_set_y_orig = np.array(train_dataset["train_set_y"][:]) # метки классов тренировочных данных
test_dataset = h5py.File('./test_catvnoncat.h5', "r")
test_set_x_orig = np.array(test_dataset["test_set_x"][:]) # признаки тестовых данных
test_set_y_orig = np.array(test_dataset["test_set_y"][:]) # метки классов тестовых данных
classes = np.array(test_dataset["list_classes"][:]) # список классов
train_set_y_orig = train_set_y_orig.reshape((1, train_set_y_orig.shape[0]))
test_set_y_orig = test_set_y_orig.reshape((1, test_set_y_orig.shape[0]))
return train_set_x_orig, train_set_y_orig, test_set_x_orig, test_set_y_orig, classesФункция load_data загружает тренировочные и тестовые данные train_catvnoncat.h5 и test_catvnoncat.h5, соответственно. Также она возвращает X и Y для каждого из набора данных, где метки классов находятся в Y, а свойства — в X. Форма изображений имеет формат (номер образца, высота в пикселях, ширина в пикселях, измерение). Так как изображения цветные, в формате RGB, они трёхмерные, их размер 64х64, а количество тренировочных образцов составляет 209.
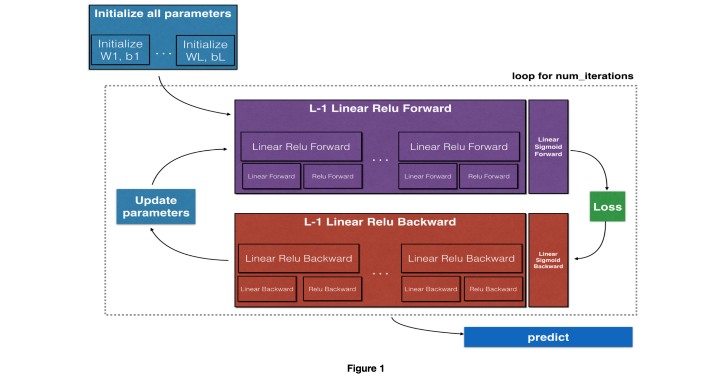 Схема работы
Схема работыМы начнём с этих задач:
- Инициализация параметров, то есть, весов и смещения
- Создание сигмоидной функции и reLU
- Создание N-слойной модели сети прямого распространения
- Создание функции стоимости для модели
- Создание обратных функций сигмоиды и reLU
- Получение параметров, передающихся в обратном порядке
- Обновление весов и смещения
- Создание предсказывающей функции
Статья разбита на две части. Первая половина задач будет рассмотрена в этой, вторая будет во второй части статьи.
Инициализация параметров
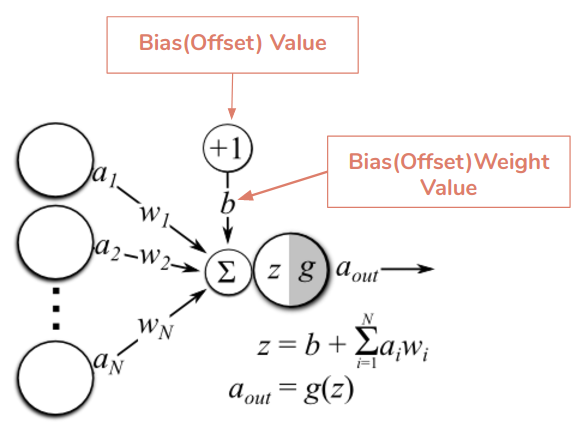 Веса и смещения
Веса и смещенияdef initialize_parameters(layer_dims):
""""
ВХОДНЫЕ ДАННЫЕ:
layers_dim: хранит измерение каждого скрытого слоя нейронной сети, индекс обозначает номер слоя, layers_dim[i] обозначает количество нейронов в i-том слое
RETURN: возвращает инициализированные параметры от W1,b1 до Wl-1,bl-1, где l = длина массива layers_dim, размер Wi (L[i], L[i-1])
"""
parameters = {}
L = len(layer_dims)
for l in range(1,L):
parameters['W' + str(l)] = np.random.randn(layer_dims[l], layer_dims[l-1]) / np.sqrt(layer_dims[l-1]) #*0.01
parameters['b' + str(l)] = np.zeros((layer_dims[l], 1))
assert(parameters['W' + str(l)].shape == (layer_dims[l], layer_dims[l-1]))
assert(parameters['b' + str(l)].shape == (layer_dims[l], 1))
return parametersФункция генерирует случайные числа для W(веса) и b(смещения) и хранит их в словаре. layers_dim — список, хранящий измерение каждого слоя и количество слоёв нейронной сети.
Сигмоида и reLU
def linear_forward(W,A,b):
"""
Имплементацияdef linear_forward(W,A,b):
"""
Имплементация линейной части прямой передачи сигнала в слоях.
ВХОДНЫЕ ДАННЫЕ:
A -- активация предыдущего слоя (или входные данные): (размер предыдущего слоя, количество примеров)
W -- матрица весов: массив numpy размера (размер текущего слоя, размер предыдущего слоя)
b -- вектор смещения, массив numpy размера (размер текущего слоя, 1)
ВЫХОДНЫЕ ДАННЫЕ:
Z -- входной параметр функции активации, также называется параметром пре-активации
cache -- словарь с ключами "A", "W", "b"; хранится для более удобной и эффективной обратной передачи
"""
Z = W.dot(A) + b
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (W,A,b)
return Z, cache
def sigmoid(Z):
"""
ВХОДНЫЕ ДАННЫЕ:
Z: WX+b
ВЫХОДНЫЕ ДАННЫЕ:
σ(Z)=σ(WA+b) =1/1+(e−(Z))
"""
A = 1/(1+np.exp(-Z))
return A, Z
def relu(Z):
"""
ВХОДНЫЕ ДАННЫЕ:
Z: WX+b
ВЫХОДНЫЕ ДАННЫЕ:
максимум из 0 и Z
"""
A = np.maximum(0,Z)
assert(A.shape == Z.shape)
cache = Z
return A, cache линейной части прямой передачи сигнала в слоях.
ВХОДНЫЕ ДАННЫЕ:
A -- активация предыдущего слоя (или входные данные): (размер предыдущего слоя, количество примеров)
W -- матрица весов: массив numpy размера (размер текущего слоя, размер предыдущего слоя)
b -- вектор смещения, массив numpy размера (размер текущего слоя, 1)
ВЫХОДНЫЕ ДАННЫЕ:
Z -- входной параметр функции активации, также называется параметром пре-активации
cache -- словарь с ключами "A", "W", "b"; хранится для более удобной и эффективной обратной передачи
"""
Z = W.dot(A) + b
assert(Z.shape == (W.shape[0], A.shape[1]))
cache = (W,A,b)
return Z, cache
def sigmoid(Z):
"""
ВХОДНЫЕ ДАННЫЕ:
Z: WX+b
ВЫХОДНЫЕ ДАННЫЕ:
σ(Z)=σ(WA+b) =1/1+(e−(Z))
"""
A = 1/(1+np.exp(-Z))
return A, Z
def relu(Z):
"""
ВХОДНЫЕ ДАННЫЕ:
Z: WX+b
ВЫХОДНЫЕ ДАННЫЕ:
максимум из 0 и Z
"""
A = np.maximum(0,Z)
assert(A.shape == Z.shape)
cache = Z
return A, cacheТаким образом, Z = W.A +b, где A = g(Z). Тогда, например, для второго слоя: Z2 = W2. A1 +b2 и A2 = g(Z2).
ReLU — это нелинейная функция активации, которая ограничивает Z нулём снизу. На данный момент это самая часто используемая функция активации. Она используется для свёрточных нейронных сетей и глубокого обучения для всех слоёв, помимо выходного. Для выходного же слоя используется сигмоида, так как её область значений (0, 1), что гораздо лучше для задач классификации.
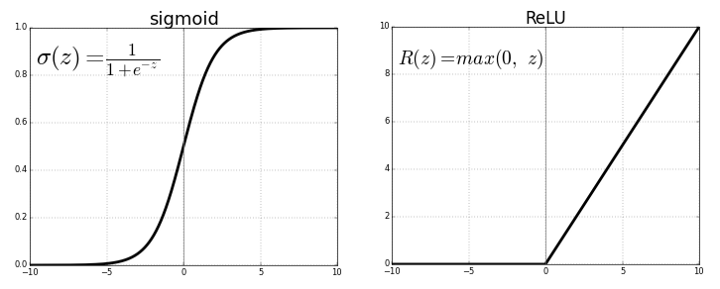 Сигмоида и reLU
Сигмоида и reLUN-слойная модель сети прямого распространения
def linear_activation_forward(W,A_prev,b, activation):
"""
Имплементация линейной части прямой передачи сигнала в слоях.
ВХОДНЫЕ ДАННЫЕ:
A_prev -- активация предыдущего слоя (или входные данные): (размер предыдущего слоя, количество примеров)
W -- матрица весов: массив numpy размера (размер текущего слоя, размер предыдущего слоя)
b -- вектор смещения, массив numpy размера (размер текущего слоя, 1)
activation -- сигмоида или reLU
ВЫХОДНЫЕ ДАННЫЕ:
A -- активация для следующего слоя
cache -- словарь, содержащий Linear_cache, activation_cache ; хранится для более удобной и эффективной обратной передачи
"""
if activation == 'relu':
Z,Linear_cache = linear_forward(W,A_prev,b)
A,activation_cache = relu(Z)
if activation == 'sigmoid':
Z,Linear_cache = linear_forward(W,A_prev,b)
A,activation_cache = sigmoid(Z)
cache = (Linear_cache, activation_cache)
return A, cache
def L_model_forward(X, parameters):
"""
Имплементация прямой передачи для произведения вычислений [LINEAR->RELU]*(L-1)->LINEAR->SIGMOID
ВХОДНЫЕ ДАННЫЕ:
X -- данные, массив numpy размера (размер входных данных, количество примеров)
layers_dim: хранит измерение каждого скрытого слоя нейронной сети, индекс обозначает номер слоя, layers_dim[i] обозначает количество нейронов в i-том слое
ВЫХОДНЫЕ ДАННЫЕ:
AL -- последнее пост-активационное значение
caches -- список, содержащий каждый из кэшей linear_activation_forward() (их количество L-1, индексы от 0 до L-1)
"""
caches = []
A = X # A - входной слой
L = len(parameters)//2 # деление нужно, так как parameters содержит как W, так и b для каждого слоя
# Так как единственный слой, в котором используется сигмоида - выходной, все остальные слои (от 1 до L-1) используют функцию reLU
for l in range(1,L):
A_prev = A
A, cache = linear_activation_forward(parameters['W'+str(l)],A_prev,parameters['b'+str(l)],activation ='relu')
caches.append(cache)
# для выходного слоя, где нужная сигмоида
Al, cache = linear_activation_forward(parameters['W'+str(L)],A,parameters['b'+str(L)],activation ='sigmoid')
caches.append(cache)
return Al, cachesФункция L_model_forward принимает на вход два аргумента: входные изображения (упорядоченные) и инициализированные параметры в виде словаря. Возвращает она активацию для следующего слоя и caches — кортеж, содержащий предыдущие линейные и активированные данные. Он поможет нам в построении обратной связи.
Вычисление потерь
Теперь, когда у нас есть предсказания, нам надо проверить их отличие от настоящих значений, то есть потерю или ошибку. В этом случае это не среднеквадратичная ошибка, так как наша функция (сигмоида) нелинейна. Если мы будем возводить ошибки в квадрат, то получим невыпуклую функцию с большим количеством локальных минимумов. Поэтому будем использовать бинарную перекрёстную энтропию(метод логарифмического правдоподобия для оценки погрешности), эта функция стоимости выпуклая, поэтому достичь глобального минимума будет достаточно легко. Вот функция стоимости и код, где m — это количество тренировочных примеров:
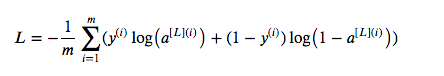 Перекрёстная энтропия
Перекрёстная энтропияdef compute_cost(Al, Y):
"""
ВХОДНЫЕ ДАННЫЕ:
AL -- вектор вероятности, соответствующий меткам предсказаний, размер: (1, количество примеров)
Y -- вектор верных меток (например, 0 для не котов и 1 для котов), размер: (1, количество примеров)
ВЫХОДНЫЕ ДАННЫЕ:
cost -- стоимости перекрёстной энтропии
"""
m = Y.shape[1]
cost = -1/m * np.sum(np.multiply(Y, np.log(Al)) + np.multiply((1-Y), np.log(1-Al)))
cost = np.squeeze(cost)
return costСледующими шагами будет обратная передача данных и объединение функций в одно целое для построения модели.
Специально для сайта ITWORLD.UZ. Новость взята с сайта NOP::Nuances of programming
